|
Société de Calcul Mathématique SA |
|
Robust mathematical modeling -4-
We give here some reflexion themes, about mathematical modeling for everyday life.
Can we model everyday life preoccupations ?
The examples we give here are valid for everyone: they can be understood by a schoolboy as well as by a professional scientist. They have a meaning for the one who studied literature, as well as for the one who went to an engineering school. Each of us will put the problem in his own terms and will bring his own answers.
Let's be clear from the very beginning: we do not claim that people should use mathematical modeling in everyday life. Conversely, all our examples below show that it would be almost impossible to establish correctly, very heavy and painful to operate, and very boring for all of us. None of us would like to do it regularly !
Our conclusion is just the opposite: our mathematical formulations should take their inspiration from the usual decision process, which is fast and coarse. We need to find an equilibrium between a precise model, which is of very little use and cannot be done in practice, and a totally empirical model, where all decisions are taken in an arbitrary manner. The search for this equilibrium is difficult ; this is precisely the objective of our program "Robust Mathematical Modeling".
A. To take a decision
1. Choice of an itinerary between two cities
Let's assume you have the choice between two itineraries in order to go to another city: one of them uses a highway (sometimes with toll), the other one normal roads. Of course, this is a simplified situation: in general, many more choices are possible.Could you, in this simplified case, write the list of all parameters which may influence your choice ? Think of it a second, and you'll come with the conclusion that you cannot write a complete list. Indeed, the list may get longer and longer, and the order of parameters will not be the same for one person and for another. One, for instance, will put first the fact that, on the highway, the risk for an accident is lower. Another person will prefer little roads, since they will make longer trips, thus allowing to arrive later. But anyway, try to come out with 25 pertinent parameters and put them in any order you like.
Examples of parameters (H : highway, R : road)
- Gain time : H
- Save money (no toll) : R
- We don't want to arrive too early : R
- Minimize the risk for a traffic accident : H
- The car is too old to go fast : R
- We want to take an itinerary we already know : H or R
- We want to take a new itinerary : H or R
- We want to go through a precise place : H or R
- We have a specific duty to perform : H or R
- We think we might need a doctor : R
- We want to avoid traffic jams : H or R
- We like to go slowly : R
- We like to look at nature, cities, villages : R
- We want to recall some souvenirs : H or R
- We like to drive at constant speed, listening to music : H
- We like to take hitch-hikers : H or R
- We make our choice according to the weather : H or R
- There are climatic differences between the two itineraries : H or R
- Someone gave us an advice, for one of the itineraries : H or R
- We followed the trafic signals : H or R
- We could not find the access to the highway : R
- We do not have money with us for the talls, nor a credit card : R
- We like to go fast : H
- We want to avoid the radars : H or R
- We care how clean the restrooms are : H
- We need to stop frequently : H
- We want to pay the fuel as little as possible : R
- We care about CO2 emissions : H or R
- We want to do the whole trip in one night, so children will sleep : H
- We want to divide the trip in small portions : R
So, as we see, we can quite easily find a large number of parameters, which may influence our choice. But the human brain does not ask all these questions, and even it finds them boring ! None of us would accept to make a "check list" of that type before we take our vacations. Our decisions are quickly taken, using a very small number of criteria, to which we give an emotional value, largely coming from previous experiences. As Von Neumann noticed ("The Computer and the Brain", 1957), the decision methods in the human brain differ fundamentally from mathematical optimization.
2. Plane or car ?
You have a trip to make, around 600 miles. Will you take your car, or will you take the plane ? Try to list correctly all the costs associated with each choice, between the moment you leave and the moment you return.
Here again, a complete list is almost impossible. If you take the plane, you must add all transportation costs at your arrival point (taxis, car rental, and so on), including fuel, parkings, tolls. You must take into account the parking cost for your own car, if you left it. Conversely, if you took your car, you must take into account the aging, the risks for an accident, a robbery, and so on.
Some of these costs are certain (fuel, for instance), but other depend on a probability (breakdown, accident, traffic ticket). These probabilities are themselves very hard to establish.
So, once again, we see that a rational decision, taken on the basis of all necessary information, is almost impossible. However, we do not ask ourselves all these questions, and we quickly decide whether we take the plane or the car (or the train !)
3. How do we get dressed ?
You are leaving for a week, and of course you must take with you some clothes. Which ones ? A rational choice will be made on probabilistic criteria: what temperature are we going to have ? Will you be invited to some dinners ? Will you meet new people ? Do you foresee working days, excursions ? And finally, of course, there are volume and weight constraints.
Try to make a list of all criteria you might want to take into account, and try to give a probability to each of them. Try to do this as completely as possible. You will not succeed, and you will become angry !
4. Waiting for the bus
You wait for the bus, but the bus does not come. You have no way to know if it is just late, or if it had an accident, or was canceled for some reason, strike or whatever. People who were waiting with you leave one after the other. Will you keep waiting, or will you leave ? On what criteria will you take your decision ?
B. Evaluate whether an action was efficient
1. Are prayers efficient ?
Did any one ever ask, using appropriate statistical techniques, whether prayers were efficient ? Do those who pray, no matter which god, get a reward for these prayers ? Are their wishes fulfilled ? One tests the efficiency of a drug ; the same question may apply to a prayer, a request.
2. Translations
Anyone would like that the translation from a language A to a language B should be biunivocal : any idea in A should correspond to an idea in B and just one. And if we start from B, the converse application should return the sentence we started with : this is the ideal model, coming from the definition of a mathematical bijection.
Unfortunately, this is not the case, even for languages as close to each other as French and Italian. Each language has its own ideas, which can be exactly translated in no other language. Any translation is an approximation. It never gives completely the cultural ideas of facts which are proper to any language, the connotations, understatements, references, and so on.
This is specially true if the two languages are far apart. Champollion, using the Rosette Stone, thought he could decifer the hieroglyphs. But how do we know that the three texts on the Stone were exactly identical translations, in three different languages ? They might be just adaptations, to three different situations, and not translations. Moreover, this unique reference is quite unsufficient to cover all writings from ancient Egypt. Let's say that the Egyptologists agreed upon the sense they want to give to the hieroglyphs, but, taking into account the small quantity of available information, we may be sure that mistakes are numerous.
Of course, the specialists will never agree, and will argue that they are the experts, and that we know nothing in hieroglyphs, but this is precisely the role of the mathematician : with no knowledge of the particular subject, he may judge that the available information is too small to avoid mistakes.
Can you come out with an English sentence which would be difficult to translate in any other language ? Try to explain why. Try to perform a classification : what are the words, the ideas, which are easy to translate, and those which are hard, and why ?
In order to help you, here is a funny example. The sentence "the flesh is weak" was submitted to an automatic translation machine (to which language, the story does not tell), and then back ; it came with "the meat is flabby".
In order to build a first model, try to work on words, not on sentences. Try to make a classification : the words which certainly have an equivalent in any other language, those which have approximate equivalents. Then try to build a mathematical model which shows this, for instance using a distance on a set.
3. Divergences of opinion
In all western countries, information is accessible to everyone, the good one as well as the bad one. So we can be surprised : how is it that people have different political opinions ? The information society in which we live should have, as a consequence, a reduction of differences in opinions. But, obviously, this is not the case : in all countries, differences between parties remain as strong as ever.
The reason is that, for this as for any real life question, human beings act in an irrational manner. Each of us basically reads only what comforts his own opinions, and buys only the newspapers that fit with his own ideas. The same way, each of us meets only with people who have similar ideas, and avoids those who would lead to questioning the acquired certainties.
Could you, on a population of given size, build a mathematical model which would show such a behavior ? To start with, we would have two opinions only, A and B, each representing half of the population. Each birth in the group A is automatically of opinion A, and the same for B, except a small proportion, which, with probability p, may pass to the opposite opinion. So we can study, as a function of the size of the population and of the probability p, the stability of both groups.
C. Irrationality of behaviors
1. The bus is waiting
You walk quietly towards the bus stop, its departure point. You know it leaves at 9:00, so you have plenty of time, and you walk slowly. But, arriving at the last intersection, when you see the bus (which is indeed waiting), you start hurrying, sometimes you run. Can you justify this behavior ?
2. Cross the street
You want to cross the street, but the small pictogram which tells the pedestrians if they can cross just passed red. You wait for a few seconds, and see that the cars did not start yet. You say : "I would have had time to cross the street", and you start crossing. Can you justify this behavior ?
3. Optimize your chances against robbery
You have a certain amount of money, for instance banknotes you took from an ATM. You are afraid of pickpockets. Will you put all notes in a single pocket, or will you distribute them between several pockets ? Try to make correctly a list of all advantages and drawbacks for each solution. Introduce some probabilities (even if they are arbitrary) for the various possible events and explain on what basis you take your decision.
4. Setting tables in a restaurant
When you go to a restaurant, you are often impressed by the amount of work, apparently useless, devoted to setting tables and then removing the dishes. For instance, if you are by yourself and sit at a table prepared for two, the waitress will remove the useless dishes. Wouldn't it be better for her to wait until the customers sit down, and then set the table according to the number of customers ? This would not slow down the service, since cooking takes time, and one has plenty of time to set the table meanwhile.
Yes, but this is true only at first sight. As a matter of fact, when they enter a restaurant, customers expect the tables to be dressed completely. They would judge negatively a restaurant for which the tables are empty when they arrive. The dishes precisely mean "We are ready to serve you". Of course, progressively, one might explain new procedures to the customers, but this would take time.
Generally speaking, for everyday's processes, one cannot just reduce to an optimization problem. One should take into account all consequences, including the human ones, as well as the weight of habits.
5. Building a house
Look at a new house, in any village, and ask yourself : among all its characteristics, how many result from a rational process ? The position on the land ? the number of rooms ? the general shape ? the aspect of doors, windows ? the type of roof ? the color of the walls ?
But first ask yourself what would be this rational process. What elements should be taken into consideration, for instance when you decide of the position of the house, or when you draw the plans. You'll find out that there are several obligations, usually due to reglementations (distance to the neighbors, height, and so on). These obligations turn into constraints, but do not result in an optimization, in the mathematical sense of the word. The decision is finally made according to tastes (which are irrational), plus some advice coming from the architect, for instance. In no stage has an optimization procedure occured.
This rules turns out to be fairly general : in everyday's life, there are many constraints, but no optimization.
D. The price of a good
People generally think that the price of a good is a well defined concept, since the economies of all countries rely upon it. But this is false.
Let's see if you are able to find a solution to the following dilemma, which comes from a true story (reproduced from SCM's Letter no 18, June 2002) :
Making gloves costs 1 dollar each pair to some company. They made 10 000 pairs and they want to export them to a country were customs rights are 4/5 of the selling price. They cannot sell the gloves more than 5 dollars each pair, due to limited buying power of consumers locally, and due to serious concurrence. How may the company realize a benefit, and how much ? We may neglect the transportation costs. We cannot cheat the customs : the declared price must be the actual selling price.
You see immediately that, if you content yourself with a simple mathematical model, there is no solution. But this is a true story, and there is a solution, truly marvelous. But this solution was not found by a professional mathematician, rather it was found by an old Jew in some ghetto, or and old Arab in a souk : people who are familiar with international commerce and know all its subtleties.
When we proposed this problem in SCM's letter, no professional mathematician found the solution. The prize we offered was won by a 13 years old girl, Anne-Sophie Aubry.
E. Errors upon measurements
When you perform a measurement, you care about the result, but not so much about the errors which may have occurred. But, quite often, the instrument is sold with an order of magnitude of the precision it gives. You know, for instance, that the thermometer you bought has a precision of 1 degree Celsius.
Now, imagine that you measure the same temperature X with three instruments, each of them having the same precision of 1 degree Celsius. You read 20°C, 20.4°C, 20.7°C. What value will you attribute to X ?
In the next situation, you draw on a paper the direction where a lighthouse can be found, but in each case an angular error was commited :
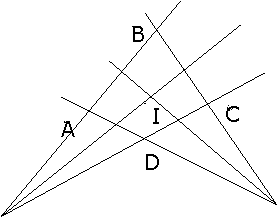
You decide that the lighthouse is at the intersection of the two sights (point I), but it might be anywhere in the intersection of the two cones (four points A, B, C, D).
The situation of two sights is very convenient, because two straight lines determine one point only, but how will you do if you have 3 sights or more ? Usually, they will not determine a single intersection point.
And, coming back to the case of two sights, you observe that the intersection point of these two lines is not the barycenter of the four points A, B, C, D.
(This application is taken from the book by Bernard Beauzamy : Modèles Mathématiques pour l'étude des phénomènes réels).
F. Putting together some resources
You are a Pharao, and you want to build a pyramid, in order to pass to posterity. For the sake of robustness, this pyramid will have a square basis. You have at your disposal an unlimited number of stones, all the same : length 1 meter, section 0,5 m x 0,5 m.
How will you dispose these stones ?
In practice, as we see on this very simple example, the choice of the criterium for optimization does not impose itself. Here, in fact, there is no such criterium. One should try to decide what one wants, and accept some compromises. But on what basis ?
To see a list of participating people and institutions to the program "Robust Mathematical Modeling", click here
Back to RMM's main page
Back to SCM's home page (English)
Back to SCM's home page (French)
Back to SCM's home page (Russian)